数据结构-散列表

散列表(Hash table)是实现字典操作的一种有效的数据结构。

简介

定义

散列表也叫哈希表，是根据键和值(key 和 value)直接进行访问的数据结构。也就是说，它通过把 key 和 value 映射到表中的一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的表叫做散列表。

给定表 M，存在函数 f(key)，对任意给定的关键字值 key，代入函数后若能得到包含该关键字的记录在表中的地址，则称表 M 为哈希表，函数 f(key) 为 哈希函数。

散列表的数据结构如下图所示：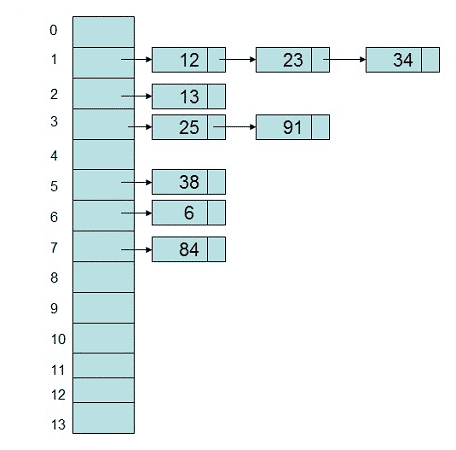

术语

• 散列函数和散列表：若关键字为 key，则其值存放在 f(key) 的存储位置上。由此，不需比较便可直接取得所查记录。称这个对应关系 f 为 散列函数，按这个思想建立的表为散列表。
• 哈希冲突：对不同的关键字可能得到同一散列地址，即 key1≠key2，而f(key1)=f(key2)，这种现象称为哈希冲突。具有相同函数值的关键字对该散列函数来说称做同义词。
• 散列和散列地址：根据散列函数 f(k) 和处理冲突的方法将一组关键字映射到一个有限的连续的地址集上，并以关键字在地址集中的“像”作为记录在表中的存储位置，这种表便称为散列表，这一映射过程称为散列造表或散列，所得的存储位置称散列地址。
• 均匀散列函数：若对于关键字集合中的任一个关键字，经散列函数映象到地址集合中任何一个地址的概率是相等的，则称此类散列函数为均匀散列函数(Uniform Hash function)，这就是使关键字经过散列函数得到一个“随机的地址”，从而减少冲突。

散列表的特点

散列表有两种用法：一种是 key 的值与 value 的值一样，一般称这种情况的结构为 Set(集合)；而如果 key 和 value 所对应的内容不一样时，那么我们称这种情况为 Map(图)。

根据散列表的存储结构，可以得出散列表的以下特点。

• 访问速度很快：由于散列表有散列函数，可以将指定的 key 都映射到一个地址上，所以在访问一个 key 对应的 value 时，根本不需要一个一个地进行查找，可以直接跳到那个地址。所以在对散列表进行添加、删除、修改、查找等任何操作时，速度都很快。
• 需要额外的空间：首先，散列表实际上是存不满的，如果一个散列表刚好能够存满，那么肯定是个巧合。而且当散列表中元素的使用率越来越高时，性能会下降，所以一般会选择扩容来解决这个问题。另外，如果有冲突的话，则也是需要额外的空间去存储的，比如链地址法，不但需要额外的空间，甚至需要使用其他数据结构。这个特点有个很常用的词可以表达，叫作“空间换时间”，在大多数时候，对于算法的实现，为了能够有更好的性能，往往会考虑牺牲些空间，让算法能够更快些。
• 无序：散列表还有一个非常明显的特点，那就是无序。为了能够更快地访问元素，散列表是根据散列函数直接找到存储地址的，这样我们的访问速度就能够更快，但是对于有序访问却没有办法应对。
• 可能会产生碰撞：没有完美的散列函数，无论如何总会产生冲突，这时就需要采用冲突解决方案，这也使散列表更加复杂。通常在不同的高级语言的实现中，对于冲突的解决方案不一定一样。

常用的哈希函数

哈希函数能使对一个数据序列的访问过程更加迅速有效，通过哈希函数，数据元素将被更快地定位。

直接寻址表

直接寻址法是指取关键字或关键字的某个线性函数值为散列地址，即 H(key)=key 或 H(key) = a*key + b，其中 a 和 b 为常数，这种散列函数叫做自身函数。

• 优点：简单、均匀，也不会产生冲突。
• 缺点：需要事先知道关键字的分布情况，适合查找表较小且连续的情况。

由于这样的限制，在现实应用中，此方法虽然简单，但却并不常用。

数字分析法

数字分析法是指分析一组数据，比如一组员工的出生年月日，这时我们发现出生年月日的前几位数字大体相同，这样的话，出现冲突的几率就会很大，但是我们发现年月日的后几位表示月份和具体日期的数字差别很大，如果用后面的数字来构成散列地址，则冲突的几率会明显降低。因此数字分析法就是找出数字的规律，尽可能利用这些数据来构造冲突几率较低的散列地址。

如果现在要存储某家公司的登记表，若用手机号作为关键字，极有可能前7位都是相同的，选择后四位成为散列地址就是不错的选择。若容易出现冲突，对抽取出来 的数字再进行反转、右环位移等。总的目的就是为了提供一个散列函数，能够合理地将关键字分配到散列表的各个位置。

数字分析法通过适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布比较均匀，就可以考虑用这个方法。

平方取中法

平方取中法是指当无法确定关键字中哪几位分布较均匀时，可以先求出关键字的平方值，然后按需要取平方值的中间几位作为哈希地址。这是因为：平方后中间几位和关键字中每一位都相关，故不同关键字会以较高的概率产生不同的哈希地址。

这个方法计算很简单，假设关键字是1234，那么它的平方就是1522756，再抽取中间的3位就是227，用做散列地址。

平方取中法比较适合不知道关键字的分布，而位数又不是很大的情况。

折叠法

折叠法是指将关键字从左到右分割成位数相同的几部分，最后一部分位数可以不同，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐，然后相加；间界叠加是从一端向另一端沿分割界来回折叠，然后对齐相加。

比如关键字是9876543210，散列表表长为三位，将它分为四组，987|654|321|0，然后将它们叠加求和987 + 654 + 321 + 0 = 1962，再求后3位得到散列地址962。

折叠法事先不需要知道关键字的分布，适合关键字位数较多的情况。

随机数法

随机数法是指选择一随机函数，取关键字的随机值作为散列地址，即 f(key)=random(key)。这里 random() 是随机函数，通常用于关键字长度不同的场合。

除留余数法

除留余数法是指取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址，即 H(key)=key mod p,p<=m，mod 是取模(求余数)。不仅可以对关键字直接取模，也可在折叠、平方取中等运算之后取模。对 p 的选择很重要，一般取素数或 m，若 p 选的不好，容易产生同义词。

总结

总之，实际工作中需视不同的情况采用不同的哈希函数，通常考虑的因素有：

• 计算哈希函数所需时间
• 关键字的长度
• 哈希表的大小
• 关键字的分布情况
• 记录的查找频率

综合以上等因素，才能决策选择哪种散列函数更合适。

哈希冲突的解决方法

有时不同的 key 通过哈希函数可能会得到相同的地址，这在操作时可能会对数据造成覆盖、丢失。之所以产生冲突是由于哈希函数有时对不同的 key 计算之后获得了相同的地址。

冲突的处理方式也有很多，下面介绍几种。

开放寻址法

开放寻址法是指一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

它的公式为：f_i(key)=(f(key)+d_i) MOD m (i=1,2，…，m-1)，其中 f(key) 为散列函数，m 为散列表长，d_i 为增量序列，可有下列三种取法：

• d_i=1,2,3，…，m-1，称线性探测再散列；
• d_i=1²,-1²,2²,-2²，…，±k²,(k<=m/2）称二次探测再散列；
• d_i=伪随机数序列，称伪随机探测再散列。

再哈希法

再哈希法是指在产生冲突之后，使用关键字的其他部分继续计算地址，如果还是有冲突，则继续使用其他部分再计算地址。

它的公式为：f_i(key)=RH_i(key) (i=1,2，…，k)，其中 RH_i(key) 就是不同的散列函数，可以把前面说的除留余数、折叠、平方取中全部用上。每当发生散列地址冲突时，就换一个散列函数计算。

这种方法能够使得关键字不产生聚集，但相应地也增加了计算的时间。

链地址法

链地址法也叫拉链法，其实就是对 key 通过哈希之后落在同一个地址上的值，做一个链表。在很多高级语言的实现当中，也是使用这种方式处理冲突的。

将所有关键字为同义词的记录存储在一个单链表中，称这种表为同义词子表，在散列表中只存储所有同义词子表前面的指针。此时，已经不存在什么冲突换地址的问题，无论有多少个冲突，都只是在当前位置给单链表增加结点的问题。

链地址法对于可能会造成很多冲突的散列函数来说，提供了绝不会出现找不到地址的保证。当然，这也就带来了查找时需要遍历单链表的性能损耗。

公共溢出区法

公共溢出区法是指是建立一个公共溢出区，当地址存在冲突时，把新的地址放在公共溢出区里。

在查找时，对给定值通过散列函数计算出散列地址后，先与基本表的相应位置进行比对，如果相等，则查找成功；如果不相等，则到溢出表中进行顺序查找。如果相对于基本表而言，有冲突的数据很少的情况下，公共溢出区的结构对查找性能来说还是非常高的。

哈希表的性能分析

在没有哈希冲突的情况下，哈希表是在查找中效率最高的，因为它的时间复杂度为 O(1)。然而在实际应用中，冲突是不可避免的，那么散列表的平均查找长度取决于那些因素呢？

• 处理冲突的方法：相同的关键字，相同的散列函数，处理冲突的方法不同，会使得平均查找长度不同。
• 哈希表的装填因子 α： α 为填入表中的记录个数/哈希表长度。α 标志着哈希表的装满程度。当填入表中的记录越多，α 越大，产生冲突的可能性就越大。也就是说哈希表的平均查找长度取决于装填因子，而不是取决于集合中的记录个数。可以通过将哈希表的空间设置的比查找集合大，通过牺牲空间，在换取查找效率。这样哈希查找的时间复杂度就是真的是 O(1) 了。

散列表的适用场景

根据散列表的特点可以想到，散列表比较适合查找性能要求高，数据元素之间无逻辑关系要求的情况。

缓存

通常开发程序时，对一些常用的信息会做缓存，用的就是散列表，比如要缓存用户的信息，一般用户的信息都会有唯一标识的字段，比如 ID。这时做缓存，可以把 ID 作为 key，而 value 用来存储用户的详细信息，这里的 value 通常是一个对象，包含用户的一些关键字段，比如名字、年龄等。

在每次需要获取一个用户的信息时，就不用与数据库这类的本地磁盘存储交互了(其实在大多数时候，数据库可能与服务不在一台机器上，还会有相应的网络性能损耗)，可以直接从内存中得到结果。这样不仅能够快速获取数据，也能够减轻数据库的压力。

有时要查询一些数据，这些数据与其他数据是有关联的，如果进行数据库的关联查询，那么效率会非常低，这时可以分为两部分进行查询：将被关联的部分放入散列表中，只需要遍历一遍；对于另一部分数据，则通过程序手动关联，速度会很快，并且由于是通过散列表的 key 和 value 的对应关系对应数据的，所以性能也会比较好。

快速查找

这里说的查找，不是排序，而是在集合中找出是否存在指定的元素。

这样的场景很多，比如要在指定的用户列表中查找是否存在指定的用户，这时就可以使用散列表了。在这个场景下使用的散列表其实是在上面提到的 Set 类型，实际上不需要 value 这个值。

还有一个场景，一般对网站的操作会有个 IP 地址黑名单，如果某些 IP 有大量的非法操作，于是就封锁了这些 IP 对我们网站的访问。这个 IP 是如何存储的呢？就是用的散列表。当一个访问行为发送过来时，通常会获取其 IP，判断其是否存在于黑名单中，如果存在，则禁止其访问。这种情况也是使用的 Set。