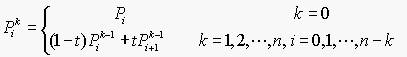Paint 常用操作
android.graphics.Paint 表示画笔,要将图像绘制在画布上,就必须先调整画笔,画笔除了可以绘制点、线、面之外,还能通过画笔绘制文字等。
| 作用描述 | 相关 API | 备注 |
|---|---|---|
| 重置画笔 | reset | 将画笔恢复到默认设置 |
| 替换画笔 | set | 用新的画笔替换到当前画笔的所有属性 |
| 设置标志 | setFlags | 设置定义好的一些标志,如抗锯齿、防抖动等 |
| 隐藏模式 | setHinting | 设置画笔的隐藏模式 |
| 抗锯齿 | setAntiAlias | 设置抗锯齿效果,设置 true 则边缘会将锯齿模糊化 |
| 防抖动 | setDither | 设置防抖动,设置 true 则图片看上去会更柔和点 |
| 画笔样式 | setStyle | 设置画笔的样式,FILL 表示填充,STROKE 表示描边,FILL_AND_STROKE 表示填充加描边 |
| 画笔颜色 | setColor、setAlpha、setARGB | 设置画笔的颜色、Alpha 值、ARGB 值 |
| 描边样式 | setStrokeWidth、setStrokeMiter、setStrokeCap、setStrokeJoin | 依次为描边的宽度、斜切值、笔帽、结合方式 |
| 着色器 | setShader | 设置或清除着色器 |
| 阴影层 | setShadowLayer、clearShadowLayer | 设置、清除阴影层 |
| 颜色过滤器 | setColorFilter | 设置或清除颜料的颜色过滤器,并返回参数 |
| 图像混合模式 | setXfermode | 设置图形重叠时的处理方式,如合并,取交集或并集 |
| 路径效果 | setPathEffect | 设置绘制轮廓的路径效果,通常使用 PathEffect 的子类 |
| 边缘效果 | setMaskFilter | 设置绘制图片的边缘效果,可以有模糊和浮雕,通常使用 MaskFilter 的子类 |
| 字体样式 | setTypeface | 设置字体样式,包括粗体、斜体、衬线体、非衬线体等 |
| 文本变换 | setTextScaleX、setTextSkewX | 设置文本的缩放比例、倾斜弧度 |
| 文本对齐方式 | setTextAlign | 设置绘画的文本对齐方式 |
| 文本特殊效果 | setUnderlineText、setStrikeThruText | 设置绘制下划线、删除线 |
| 文本字间距 | setLetterSpacing、setWordSpacing | 设置文本字间距,默认为 0,前者单位为 em,后者单位为 px |
| 文本测量 | measureText、breakText | 测量文本的宽度、字符数(如果测量的宽度超过 maxWidth,则提前停止) |
Canvas 常用操作
android.graphics.Canvas 表示画布,用于完成在 View 上的绘图。
| 作用描述 | 相关 API | 备注 |
|---|---|---|
| 绘制颜色 | drawColor、drawRGB、drawARGB | 使用单一颜色填充整个画布 |
| 绘制基本形状 | drawPoint、drawPoints、drawLine、drawLines、drawRect、drawRoundRect、drawOval、drawCircle、drawArc | 依次为点、线、矩形、圆角矩形、椭圆、圆、圆弧 |
| 绘制图片 | drawBitmap、drawPicture | 绘制位图和图片 |
| 绘制文本 | drawText、drawPosText、drawTextOnPath | 依次为绘制文字、绘制文字时指定每个文字位置、根据路径绘制文字 |
| 绘制路径 | drawPath | 绘制路径,绘制贝塞尔曲线时也需要用到该函数 |
| 顶点操作 | drawVertices、drawBitmapMesh | 通过对顶点操作可以使图像形变,drawVertices 直接对画布作用、drawBitmapMesh 只对绘制的 Bitmap 作用 |
| 画布剪裁 | clipPath、clipRect | 设置画布的显示区域 |
| 画布快照 | save、restore、saveLayerXxx、restoreToCount、getSaveCount | 依次为保存当前状态、回滚到上一次保存的状态、保存图层状态、会滚到指定状态、获取保存次数 |
| 画布变换 | translate、scale、rotate、skew | 依次为位移、缩放、旋转、错切 |
| Matrix(矩阵) | getMatrix、setMatrix、concat | 实际画布的位移,缩放等操作的都是图像矩阵 Matrix,只不过 Matrix 比较难以理解和使用,故封装了一些常用的方法 |
Path 常用操作
android.graphics.Path 表示路径,封装了一些复合的几何路径,其中包括直线、二次曲线、三次曲线等几何路径,它可以通过 canvas.drawPath(path, paint) 方法完成绘图。
| 作用描述 | 相关 API | 备注 |
|---|---|---|
| 移动起点 | moveTo | 移动下一次操作的起点位置 |
| 设置终点 | setLastPoint | 重置当前 Path 中最后一个点位置,如果在绘制之前调用,效果和 moveTo 相同 |
| 连接直线 | lineTo | 添加上一个点到当前点之间的直线到 Path |
| 闭合路径 | close | 连接第一个点连接到最后一个点,形成一个闭合区域 |
| 添加内容 | addRect、addRoundRect、addOval、addCircle、addPath、addArc、arcTo | 添加(矩形、圆角矩形、椭圆、圆、路径、圆弧)到当前 Path (注意 addArc 和 arcTo 的区别) |
| 是否为空 | isEmpty | 判断 Path 是否为空 |
| 是否为矩形 | isRect | 判断 Path 是否是一个矩形 |
| 替换路径 | set | 用新的路径替换到当前路径所有内容 |
| 偏移路径 | offset | 对当前路径之前的操作进行偏移(不会影响之后的操作) |
| 贝塞尔曲线 | quadTo、cubicTo | 分别为二次和三次贝塞尔曲线的方法 |
| rXxx方法 | rMoveTo、rLineTo、rQuadTo、rCubicTo | 不带 r 的方法是基于原点的坐标系(偏移量),rXxx 方法是基于当前点坐标系(偏移量) |
| 填充模式 | setFillType、getFillType、isInverseFillType、toggleInverseFillType | 设置、获取、判断和切换填充模式 |
| 提示方法 | incReserve | 提示 Path 还有多少个点等待加入(这个方法貌似会让Path优化存储结构) |
| 布尔操作 | op | 对两个 Path 进行布尔运算(即取交集、并集等操作) |
| 计算边界 | computeBounds | 计算 Path 的边界 |
| 重置路径 | reset、rewind | 清除 Path 中的内容 reset 不保留内部数据结构,但会保留 FillType;rewind 会保留内部的数据结构,但不保留 FillType |
| 矩阵操作 | transform | 矩阵变换 |
Matrix 常用操作
android.graphics.Matrix 表示矩阵,它本身不能对图像或 View 进行变换,但它可与其他 API 结合来控制图形、View 的变换,如 Canvas。
| 作用描述 | 相关 API | 备注 |
|---|---|---|
| 基本方法 | equals、hashCode、toString、toShortString | 比较、获取哈希值、转换为字符串 |
| 数值操作 | set、reset、setValues、getValues | 设置、重置、设置数值、获取数值 |
| 数值计算 | mapPoints、mapRadius、mapRect、mapVectors | 计算变换后的数值 |
| 设置(set) | setConcat、setRotate、setScale、setSkew、setTranslate | 设置变换 |
| 前乘(pre) | preConcat、preRotate、preScale、preSkew、preTranslate | 前乘变换 |
| 后乘(post) | postConcat、postRotate、postScale、postSkew、postTranslate | 后乘变换 |
| 特殊方法 | setPolyToPoly、setRectToRect、rectStaysRect、setSinCos | 一些特殊操作 |
| 矩阵相关 | invert、isAffine(API21)、isIdentity | 求逆矩阵、是否为仿射矩阵、是否为单位矩阵 |
贝塞尔曲线常用操作
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。
曲线定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。
| 贝塞尔曲线 | 相关 API | 演示动画 |
|---|---|---|
| 一阶曲线 | lineTo | 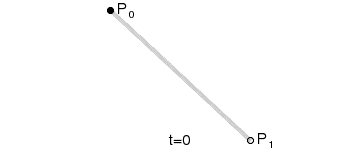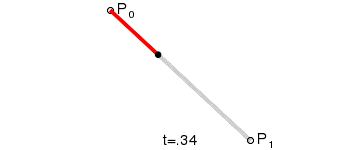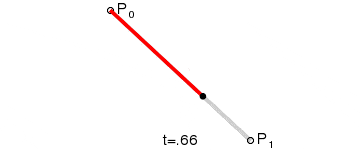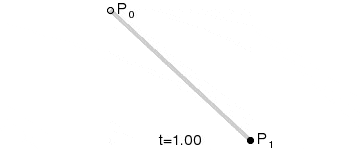 |
| 二阶曲线 | quadTo | 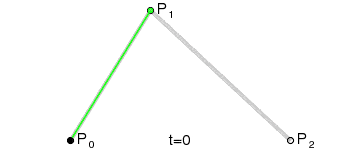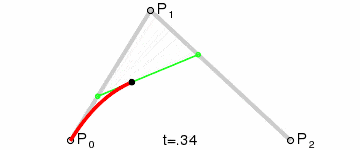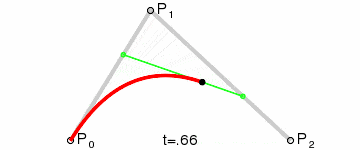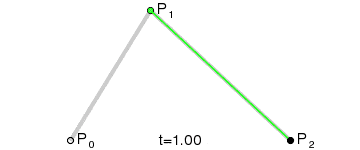 |
| 三阶曲线 | cubicTo | 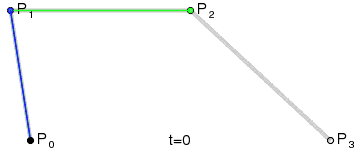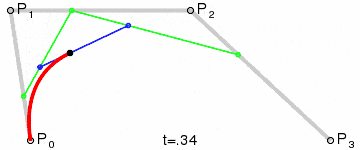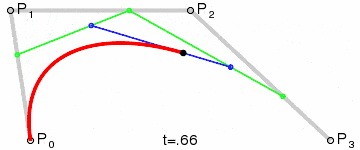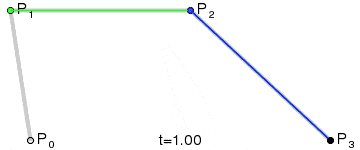 |
| 四阶曲线 | 无 | 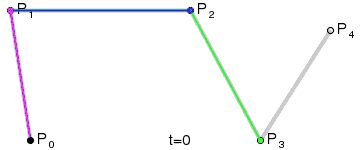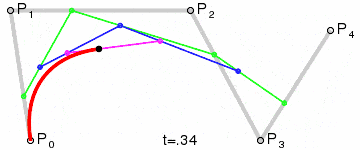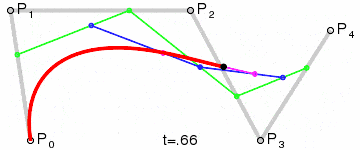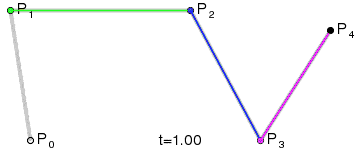 |
| 五阶曲线 | 无 | 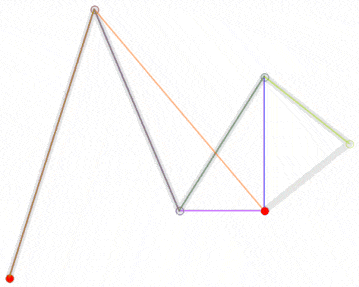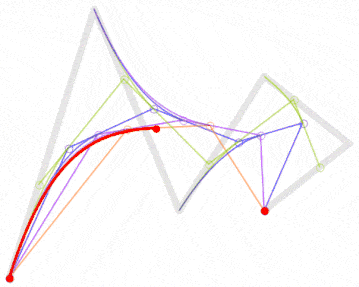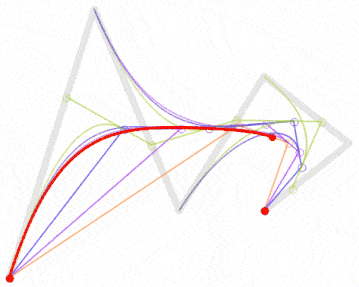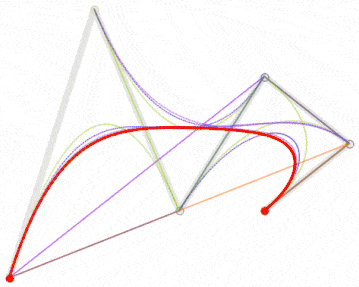 |
原理和公式
下面介绍一下贝塞尔曲线的原理和公式:
以下公式中:B(t)为 t 时间下点的坐标;P0 为起点,Pn 为终点,Pi 为控制点。
一阶贝塞尔曲线(线段)
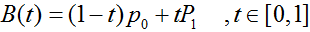

原理:由 P0 至 P1 的连续点, 描述的一条线段
二阶贝塞尔曲线(抛物线)
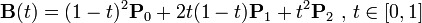

原理:由 P0 至 P1 的连续点 Q0,描述一条线段。
由 P1 至 P2 的连续点 Q1,描述一条线段。
由 Q0 至 Q1 的连续点 B(t),描述一条二次贝塞尔曲线。
经验:P1-P0为曲线在P0处的切线。
三阶贝塞尔曲线
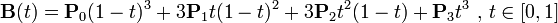

四阶贝塞尔曲线

五阶贝塞尔曲线

通用公式